 |
The Binomial Theoram |
Description:
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power (x + y)n into a sum involving terms of the form a xb yc, where the exponents b and c are nonnegative integers with b + c = n, and the coefficient a of each term is a specific positive integer depending on n and b. For example,
The coefficient a in the term of a xb yc is known as the binomial coefficient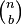 
or 
(the two have the same value). These coefficients for varying n and b can be arranged to form Pascal's triangle. These numbers also arise in combinatorics, where 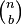gives the number of different combinations of b elements that can be chosen from an n-element set.
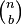or (the two have the same value). These coefficients for varying n and b can be arranged to form Pascal's triangle. These numbers also arise in combinatorics, where 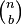gives the number of different combinations of b elements that can be chosen from an n-element set.Statement of the theorem[edit]
According to the theorem, it is possible to expand any power of x + y into a sum of the form
where each 
is a specific positive integer known as a binomial coefficient. (When an exponent is zero, the corresponding power expression is taken to be 1 and this multiplicative factor is often omitted from the term. Hence one often sees the right side written as 
.) This formula is also referred to as the binomial formula or the binomial identity. Using summation notation, it can be written as
is a specific positive integer known as a binomial coefficient. (When an exponent is zero, the corresponding power expression is taken to be 1 and this multiplicative factor is often omitted from the term. Hence one often sees the right side written as .) This formula is also referred to as the binomial formula or the binomial identity. Using summation notation, it can be written as
The final expression follows from the previous one by the symmetry of x and y in the first expression, and by comparison it follows that the sequence of binomial coefficients in the formula is symmetrical. A simple variant of the binomial formula is obtained by substituting 1 for y, so that it involves only a single variable. In this form, the formula reads
or equivalently
